В какой системе счисления работает компьютер
Однажды я прочитал в интернете про троичную систему счисления и заинтересовался. Меня мучил вопрос, а нельзя использовать в основе компьютера симметричную троичную систему счисления (СС), и даже вдруг это увеличит производительность компьютера? Мне казалось, что это возможно, и я жаждал это проверить.
Информация:
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры , а в симметричной троичной системе счисления знаки , .
У некоторых людей эта логика вызывает затруднения. Они говорят, например, приведите пример подобной логики в жизни.
Человек, немного подумавший над этой логикой поймет, что она более жизненна чем двоичная. Обычный пример троичной логики в жизни связан с постоянным током: ток движется в одну сторону, в другую сторону, его нет.
Оказалось, что симметричная троичная система счисления использовалась давным-давно для решения «задачи о гирях», использовалась в компьютере Сетунь, построенном в 50-е годы в МГУ. С 2008 года в университете « California Polytechnic State University of San Luis Obispo» функционирует цифровая компьютерная система TCA2, основанная на троичной системе счисления.
В чем же плюсы троичной СС над двоичной? Рассмотрим эти плюсы:
Квантовые компьютеры
Итог:
В конечном итоге видно, что троичная симметричная система лучше двоичной системы в некоторых показателях, но не сильно выигрывает. Но с пришествием квантовых компьютеров троичные вычисления получили новую жизнь. Универсальные квантовые логические вентили — краеугольный камень новорожденных квантовых вычислительных систем — требует сотни вентилей для завершения одной полезной операции. Квантовый компьютер канадской компании D-Wave, анонсированный в прошлом году, состоит всего из 16 квантовых битов — кубитов — минимум, необходимый для управляемого вентиля «NOT». Использование в квантовом компьютере кутритов нужно было бы намного меньше вентилей для завершения одной операции. Я думаю, если бы началось производство и тестирование таких компьютеров, то результаты были бы лучше, чем у обычных компьютеров, вскоре началось бы массовое их производство, и про двоичные компьютеры все бы забыли…
Изучение систем счисления, которые используются в компьютерах, важно для понимания того, каким образом производится обработка числовых данных в ЭВМ.
Система счисления — способ записи чисел с помощью заданного набора специальных символов (цифр) и сопоставления этим записям реальных значений. Все системы счисления можно разделить на непозиционные и позиционные. В непозиционных системах счисления, которые появились значительно раньше позиционных, смысл каждого символа не зависит от того места, на котором он стоит. Примером такой системы счисления является римская, в которой для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква — V пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т.д. Например, число 264 записывается в виде CCLXIV. Недостатком непозиционных систем является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. Правила выполнения вычислений с многозначными числами в позиционной системе счисления были разработаны средневековым математиком Мухамедом аль-Хорезми и в Европе были названы алгоритмами (от латинского написания имени аль-Хорезми – Algorithmi).
В вычислительной технике применяются позиционные системы счисления . Позиционных систем счисления существует множество и отличаются они друг от друга алфавитом — множеством используемых цифр. Размер алфавита (число цифр в нем) называется основанием системы счисления. Последовательная запись символов алфавита (цифр) изображает число. Позиция символа в изображении числа называется разрядом. Разряду с номером 0 соответствует младший разряд целой части числа. Каждому символу соответствует определенное число, которое меньше основания системы счисления. В зависимости от позиции (разряда) числа значение символа умножается на степень основания, показатель которой равен номеру разряда.
Таким образом, целое положительное число А в позиционной системе счисления можно представить выражением:
или , где p — основание системы счисления, целое положительное число; a — cимвол (цифра); n — номер старшего разряда числа.
Обозначения цифр берутся из алфавита, который содержит p символов. Каждой цифре соответствует определенный количественный эквивалент. Обозначение ak следует понимать как цифру в k-м разряде. Всегда выполняется неравенство: ak
Запись A(p) указывает, что число А представлено в системе счисления с основанием р:
Примером системы счисления является всем нам хорошо известная десятичная система счисления. Любое число в ней записывается с помощью цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Важно, что значение каждой цифры зависит от того места, на котором она стоит в этой записи. Например, 1575: цифра 5 в записи числа встречается дважды: цифра 5 в последнем разряде — число единиц, а цифра 5, находящаяся в записи числа левее, — число сотен. Т.к. значение каждой цифры (ее "вес") определяется той позицией, которую цифра занимает в записи числа, то система счисления называется позиционной. В десятичной системе счисления значение единицы каждого разряда в 10 раз больше единицы соседнего с ним правого разряда.
Само число 10 называется основанием системы счисления, а цифры, используемые в десятичной системе — базисными числами этой системы.
Но в качестве основания системы счисления можно выбрать любое целое число. Чтобы отличить, в какой системе счисления записано число, будем указывать основание системы счисления в виде индекса в десятичной системе счисления, заключенного в круглые скобки. Если основание системы счисления равно 10 или очевидно из контекста, то индекс будет опущен.
В компьютере для представления информации используются десятичная, двоичная и шестнадцатеричная системы счисления. Количество цифр, которое требуется для изображения числа в позиционной системе счисления , равно основанию системы счисления р. Например, для записи чисел в двоичной системе счисления требуется две цифры, в десятичной — десять, а в шестнадцатеричной — шестнадцать.
Двоичная система счисления имеет набор цифр , р=2. В общем виде, используя формулу (1), двоичное число можно представить выражением:
Например, число 101101(2) можно записать так:
101101(2) = 1*2 5 +0*2 4 +1*2 3 +1*2 2 +0*2 1 +1*2 0
Двоичная система счисления имеет особую значимость в информатике: внутреннее представление любой информации в компьютере является двоичным, т.е. описывается набором символов только из двух знаков 0 и 1.
Шестнадцатеричная система счисления имеет набор цифр , p = 16. Для изображения чисел в шестнадцатеричной системе счисления требуются 16 цифр. Для обозначения первых десяти цифр используются цифры десятичной системы счисления, шесть остальных — первых шесть прописных букв латинского алфавита. По формуле (1) шестнадцатеричное число может быть представлено так:
1. Число E7F8140 по формуле (4) запишется так:
Представление информации, хранящейся в памяти компьютера, в ее истинном двоичном виде весьма громоздко из-за большого количества цифр. Поэтому при записи такой информации на бумаге или выводе ее на экран принято использовать восьмеричную или шестнадцатеричную системы счисления. В современных компьютерах чаще используется шестнадцатеричная система счисления.
Полезно помнить некоторые степени двойки и шестнадцати.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 k | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
| 16 k | 16 | 256 | 4096 | 65536 | 1048576 |
Соответствие чисел в различных системах счисления
| Десятичная | Шестнадцатеричная | Двоичная |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
Арифметические операции, выполняемые в позиционных системах счисления
В вычислительной технике наиболее часто выполняется операция сложения. Пусть заданы два целых положительных числа в позиционной системе счисления с основанием р. Запишем эти числа в виде:
Сумма этих чисел равна числу, которое может быть записано в аналогичном виде:
Вычисления выполняются по следующим правилам:
- операция сложения выполняется поразрядно, начиная с младших разрядов в слагаемых;
- в каждом одноименном разряде слагаемых суммируются соответствующие цифры и перенос из предыдущего разряда суммы;
- если сумма цифр одноименных разрядов слагаемых и переноса меньше основания системы счисления, то перенос в следующий разряд равен нулю, если равна или больше — то равен единице.
В качестве примера рассмотрим арифметические операции в двоичной системе счисления.
Арифметические операции над числами в двоичной системе счисления
Рассмотрим правила выполнения арифметических операций над однозначными числами. Представим их в виде таблиц.
| Правила сложения | Правила вычитания | Правила умножения |
| 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 | 0 - 0 = 0 0 - 1 = -1 1 - 0 = 1 1 - 1 = 0 | 0 * 0 = 0 1 * 0 = 0 0 * 1 = 0 1 * 1 = 1 |
2. Найти разность двух чисел 10101(2) и 1010(2):
3. Умножить два числа 1011(2) и 101(2):
Перевод чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
Для перевода чисел из любой системы счисления в десятичную можно воспользоваться выражением (1). Сначала в десятичную систему счисления переводится основание той системы, из которой осуществляется перевод, а затем цифры исходного числа. Результаты подставляются в выражение (1). Полученная сумма дает искомый результат.
Пример . Перевести в десятичную систему счисления числа С7(16) и 1010(2) :
С7(16) = 12*16 1 + 7*16 0 = 192 + 7 =199 (10) ;
1010 (2) = 1*2 3 + 1*2 1 = 8+2 10.
Эквивалентными являются алгоритмы для вычисления значения многочлена в некоторой точке х, заданные следующими формулами:
Запись (9) носит название вычислительной схемы Горнера.
Алгоритм, задаваемый формулой (9) требует меньше арифметических операций и сводится к выполнению последовательной цепочки операций умножения и сложения в порядке их записи слева направо, поэтому при переводе чисел в десятичную систему счисления можно воспользоваться схемой Горнера.
Чтобы перевести целую часть числа из десятичной системы счисления в систему с основанием р, необходимо разделить ее на р, остаток даст младший разряд числа. Полученное частное вновь делят на р — остаток даст следующий разряд числа и т.д.
Пример. Перевести десятичное число 25 в двоичную систему счисления:
25 : 2 = 12 (остаток 1);
12 : 2 = 6 (остаток 0),
6 : 2 = 3 (остаток 0),
3 : 2 = 1 (остаток 1),
1 : 2 = 0 (остаток 1).
Перевод чисел из десятичной системы счисления в шестнадцатеричную производится аналогично.
Для перевода целых чисел из десятичной системы счисления в систему счисления с основанием р:
- Последовательно делить заданное число и получаемые целые части на новое основание счисления (р) до тех пор, пока целая часть не станет меньше нового основания счисления.
- Полученные остатки от деления, представленные цифрами из нового счисления, записать в виде числа, начиная с последней целой части.
Преобразования чисел из двоичной в восьмеричную и шестнадцатеричную системы и наоборот просты потому, что числа 8 и 16 являются целыми степенями числа 2.
Для того, чтобы перевести число, записанное в восьмеричной системе в двоичный код, необходимо каждую цифру восьмеричного числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются. Например:
12345667(8) = 001 010 011 100 101 110 110 111(2) =
= 1 010 011 100 101 110 110 111(2).
Обратный перевод производится так: каждая триада двоичных цифр заменяется восьмеричной цифрой. Для правильного перевода число должно быть выровнено, т.е. число двоичных знаков должно быть кратно трем. Выравнивание производится простым дописыванием требуемого количества нулей перед старшим разрядом целой части числа. Например:
При переводах чисел между двоичным и шестнадцатеричным системами счисления используются четверки двоичных чисел — тетрады. При необходимости выравнивание выполняется до длины двоичного числа, кратной четырем. Например:
12345ABCDEF(16) = 1 0010 0011 0100 0101 1010 1011 1100 1101 1110 1111(2);
11001111010 1110(2) = 0110 0111 1010 1110(2) = 67AF(16).
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно используется вспомогательный, двоичный код числа. Например:
1234567(8) = 001 010 011 100 101 110 111(2)
= 0101 0011 1001 0111 0111(2) = 53977(16);
1267ABC(16) = 0001 0010 0110 0111 1010 1011 1100(2)
= 010 010 011 001 111 101 010 111 100(2) = 223175274(16).
Системы счисления
Бит, байт и размер данных
В прошлых статьях, когда мы рисовали схемы на языке LD, мы использовали тип данных BOOL. BOOL — это простейший тип данных, который может принимать всего два значения: и , они же FALSE и TRUE и содержит в себе количество информации, соответствующее одному биту. Бит — это наименьшее количество информации. Один бит равен количеству информации, получаемой в результате осуществления одного из двух равновероятных событий. Например, выпадение орла или решки при бросании монетки. Помимо бита для обозначения количества информации применяют понятие байта. В современных системах обычно имеют в виду, что байт состоит из восьми бит. При записи в качестве единицы измерения биты записываются как «бит», а байты как «Б», например, бит, Б. Как и для других единиц измерения, для записи количества информации перед единицей измерения используются десятичные приставки СИ . Кроме того, для битов и байтов используют двоичные приставки .
| Название | Обозначение | Степень |
| кило | К | |
| мега | М | |
| гига | Г | |
| терра | Т | |
| пета | П |
Например, Кбит = бит = КБ = Б.
| Название | Обозначение | Степень | Множитель |
| кибибайт | Ки (Ki) | ||
| мебибайт | Ми (Mi) | ||
| гибибайт | Ги (Gi) | ||
| тебибайт | Ти (Ti) | ||
| пебибайт | Пи (Pi) |
Например, Кибит = бит = КиБ = Б.
Иногда при написании десятичных приставок имеются в виду двоичные, то есть при записи КБ имеется в виду Б. Такое использование приставок формально хоть и не является корректным, но очень часто встречается на практике.
Также стоит отметить, что иногда под словом байт подразумевается размер регистров процессора, то есть количество бит, которое процессор может обрабатывать за раз. Размер регистров процессора называется разрядность (или битность) процессора. Из контекста всегда можно понять, что имеется в виду: бит или один разряд процессора. Современные процессоры, работающие под управлением Windows, имеют разрядность в или бита.
Системы счисления
Наверное, всем известно, что компьютеры оперируют данными в виде единиц и нолей. Такая система счисления называется двоичной позиционной. Система счисления — это способ записи цифр. Двоичная система наиболее удобна для применения в электронных схемах. Нулю соответствует отсутствие напряжения, единице — его наличие, или наоборот, в электронике достаточно часто единице соответствует отсутствие напряжение, нулю его наличие.
История знает попытки создания компьютеров на основе других систем счисления. Например, советский компьютер Сетунь , который использовал троичную систему счисления, или американский Mark I с десятичной системой. Но какого-либо серьезного распространения компьютеры, основанные на системах счисления, отличных от двоичной, не получили.
Системы счисления делятся на позиционные, непозиционные и смешанные:
- Позиционные системы счисления — системы счисления, в которых значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Например, рассмотрим число , — означает количество сотен, — количество десятков, — количество единиц. Так, арабская система счисления, которой все мы пользуемся в повседневной жизни, является десятичной позиционной системой. Обратим внимание на слово «десятичная». В данном примере оно связано с основанием системы счисления, а именно количеством знаков, используемых для записи числа в той или иной системе. В десятичной системе для записи используются цифры . Основанием является число .
- Смешанные системы счисления, — системы счисления, в которых числа, заданные в некоторой системе счисления с основанием P, изображаются с помощью цифр другой системы счисления с основанием Q, где Q
- Непозиционные системы счисления — системы счисления, в которых величина, обозначаемая цифрой, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. Примерами непозиционных счисления являются римская , египетская и система остаточных классов .
Далее в этой статье речь пойдет только о позиционных системах счисления. Как говорилось выше, в компьютерах применяют двоичную позиционную систему счисления. Для начала давайте разберемся, что такое число и чем оно отличается от цифры. Число используется для счета и выражает количество. Цифры — это набор знаков для записи чисел. В арабской системе счисления цифрами являются знаки , в двоичной — и . Каждая цифра в записи числа, называется разрядом. В информатике разряд числа считается справа налево, начиная с нуля. При записи в десятичной системе числа цифра является нулевым разрядом, цифра — первым, цифра — вторым разрядом.
Двоичная система счисления имеет основание , то есть в ней используется всего две цифры: и . Числа ноль и один в десятичной и в двоичной системах выглядят абсолютно одинаково и записываются как и соответственно. А вот цифры в двоичной системе нет, поэтому приходится добавить еще один разряд, число два в двоичной системе будет записываться как . Что бы записать число три, надо добавить к двойке единицу, выглядит это так . Для записи числа четыре снова надо добавить еще один разряд, в результате получаем . Пять записывается как и так далее.
| Десятичная | Двоичная |
Шестнадцатеричная система счисления
Двоичная система весьма неудобна для восприятия человеком. Например, число , записанное в двоичной системе, будет выглядеть как , а число соответствует записи . Для более удобного восприятия человеком числа часто представляют в шестнадцатеричной системе счисления. Переводить числа из одной системы счисления в другую мы научимся позже в этой статье.
Как и в других позиционных системах счисления, принцип записи чисел в шестнадцатеричной системе схож с рассмотренной выше двоичной системой и всем знакомой с детства десятичной. Разница лишь в том, что следующей после цифры идет (десятичная ), а новый разряд добавляется после цифры (десятичная ). В шестнадцатеричной системе счисления для записи используются следующие цифры:
| Десятичная цифра | Шестнадцатеричная цифра |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Применение именно шестнадцатеричной системы обусловлено легкостью перевода данных в нее из двоичной и обратно, а также наглядностью записи, которая обусловлена тем, что один разряд шестнадцатеричного числа эквивалентен четырем разрядам двоичного числа. То есть байт двоичного кода записывается ровно двумя цифрами шестнадцатеричного числа. Число , в двоичной системе выглядит как , а в шестнадцатеричной . Причем четыре старших разряда двоичного числа записываются шестнадцатиричной , а четыре младших разряда двоичного числа записываются шестнадцатеричным числом .
В этой статье мы используем сразу три системы счисления. Не всегда можно понять, какая система счисления применяется для записи числа, если это не указанно явно. Например, цифры могут означать три в двоичной системе, одиннадцать в десятичной и семнадцать в шестнадцатеричной. Во избежание путаницы, в математике принято указывать основание применяемой системы счисления в виде индекса после записанного числа. К примеру, запись означает, что применена двоичная система. Если индекс не указан предполагается что применена десятичная система.
При написании программ достаточно часто возникает необходимость указать в какой системе счисления записано число. В языках МЭК это делается с помощью префиксов добавляемых к числу.
Восьмеричная система хоть и поддерживается в TwinCAT, но в настоящее время почти не используется. Изложенного выше материала должно быть достаточно для ее понимания.
Перевод чисел из двоичной системы в десятичную и обратно
В сети материала со строгим изложением теоретических выкладок по переводу чисел из одной системы счисления в другую достаточно много. Здесь мы рассмотрим лишь один из удобных на практике способов перевода чисел между различными системами, несильно вдаваясь в теорию этого процесса.
В позиционных системах счисления любое число можно представить в виде где: — основание системы счисления. — числа, равные цифре, стоящей в разряде k.
Выглядит сложно, но на практике довольно просто, число можно представить в виде:
![]()
![]()
Кстати, именно из-за такой формы записи разряды чисел считают, начиная с нуля, а не с единицы.
Число (десятичное ) можно представить в виде:
![]()
![]()
Вспомнив, что можно продолжить выражение.
![]()
Можно заметить, что достаточно запомнить, какое десятичное значение соответствует каждому двоичному разряду и просуммировать их при переводе.
| Номер разряда | Двоичное значение | Десятичное значение |
Для перевода из двоичной системы в десятичную и обратно приведенную выше таблицу следует выучить наизусть.
Давайте решим несколько примеров для закрепления:
![]()
Перевод из десятичной системы в двоичную производится следующим образом: из десятичного числа вычитается ближайшее меньшее число, из только что выученной нами наизусть таблицы, и записывается соответствующие ему двоичное, после чего действие повторяется с остатком. Когда остатка не осталось, суммируем все записанные двоичные числа.
Приведем пример с числом :
Как видите, перевод из двоичной системы счисления в десятичную и обратно не составляет большой сложности.
Перевод чисел из двоичной системы в шестнадцатеричную и обратно
В целом порядок перевода в десятичную и в шестнадцатиричную систему схожи. Главное отличие в том, таблица перевода будет повторяться каждые четыре строчки, так как 16=24. Таким образом, выучив всего четыре строчки, вы сможете переводить числа любого размера.
| Номер разряда | Двоичное значение | Шестнадцатеричное значение |
Повторим некоторые примеры, которые мы приводили для десятичной системы:
![]()
![]()
Перевод из шестнадцатеричной системы в двоичную производится аналогично переводу из десятичной в двоичную, но проще, так как производится группами по 4 бита. Напомним, из шестнадцатеричного числа вычитается ближайшее меньшее число из таблицы перевода между двоичными и шестнадцатеричными числами, после чего действие повторяется с остатком. После того, как остатка не будет, суммируем все записанные двоичные числа.
Приведем пример с числом (десятичное ):
Еще один простой способ перевода чисел между системами счисления – это использование стандартного калькулятора в Windows (предварительно необходимо переключить в режим «Программист»).

Переключение калькулятора в режим «Программист»
Хотя такой способ может показаться соблазнительным, но стоит научиться переводить в уме числа хотя бы до одного байта (как читатель теперь уже может убедиться самостоятельно, в один байт можно записать числа в диапазоне от до ). С приобретением практики это станет не сложнее умножения двузначных чисел.
Экономичность системы счисления
Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p.
Мы рассмотрели троичную арифметику, теперь затронем логику:
В чем же проблемы двоичной логики?
1.Мощности компьютера, основанного на двоичной логике, не всегда хватает. Приведем пример. Одна из наиболее сложных систем защиты – криптосистема RSA. Вскрытие шифра RSA с длиной ключа 1024 бита (такая длина часто используется в информационных системах) займет в лучшем случае — при проведении распределенных вычислений на тысячах мощных ПК — не менее пятнадцати лет, а к тому времени данная система шифровки перестанет быть востребованной.
Докажем математически какая система счисления будет наилучшей для максимальной мощности и емкости памяти. Для этого рассмотрим функцию f(p)=p^(n/p), в которой p – основание системы счисления, а n – количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел, которое при этом можно записать, будет равно pn/p
f(p)=p^(n/p)
Для того, чтобы определить максимальное значение функции, найдем ее производную:
ln f = ln p^(n/p)
ln f =n/p* ln p
. (Я не буду приводить здесь всю математику)
n*p^(n/p-2) никогда не будет равно 0 => (1 — ln p)=0, ln p = 1, p = e
e = 2,71, а ближайшее целое число к нему – это три.
Значит, в этом плане лучшая система с целочисленным основанием — троичная.
Самое вкусненькое — рассмотрим троичные логические операции:
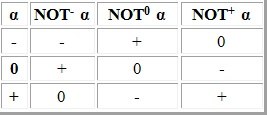
1.Отрицание

2.Конъюнкция — логическое И
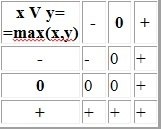
3.Дизъюнкция — логическое ИЛИ

4.Операция Выбора. Эта операция существует только для троичной логики. Таблица истинности каждой из этих трёх операций содержит везде „-“, кроме единственного значения, которое ею можно выбрать.
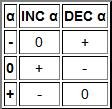
5.Модификация. Полное название этих одноместных операций: увеличение на единицу по модулю три (INC) и уменьшение на единицу по модулю три (DEC). Увеличение на единицу по модулю три – это циклическое прибавление единицы.
Здесь видны и прежде знакомые вам логические операции из двоичной логики, но добавились и новые…
Кодирование информации
В качестве наименьшей единицы измерения информации принят 1 бит. 1 бит соответствует одному разряду в двоичной системе счисления. Эта система лежит в основе архитектуры компьютеров. Для представления всего многообразия величин в компьютере объединяют несколько двоичных разрядов. Поэтому более крупными единицами измерения И в компьютере являются: 1 байт = 8 бит; 1 Кбайт=210 байт; 1 Мбайт = 210 Кбайт; 1 Гбайт = 210 Мбайт.
Поскольку информация в компьютере хранится в дискретной форме, для ее записи используется некоторый конечный набор знаков, называемый алфавитом. Очень часто в качестве алфавита используется таблица кодов, содержащая около 256 знаков. Каждому знаку соответствует числовой код. Этот код хранит образ соответствующего знака в памяти компьютера. Для понимания системы кодирования информации необходимо рассмотреть правила преобразования числовых кодов в различные системы счисления.
Наиболее популярна таблица кодов ASCII. Она состоит из 16 строк и 16 столбцов, пронумерованных от 0 до F в 16-ричной системе счисления. Например, в столбце 4 и строке D таблицы расположена заглавная буква М латинского алфавита. Таким образом при записи текста с такой буквой, она будет храниться в памяти в виде кода 4D(16) или 77(10). Другие коды: "," - 2C; "j" - 6A; "2" - 32. Обычно последние 8 столбцов таблицы кодов содержат буквы национальных алфавитов, графические знаки. В большом количестве разновидностей таблицы кодов ASCII первая половина таблицы является неизменной, а вторая - переменной.
Числа кодируются особым образом. Например, целое число, в зависимости от типа, может кодироваться одним, двумя или четырьмя байтами. Для получения кода положительного целого числа достаточно перевести его из десятичной в двоичную систему счисления, например, десятичное число 12 кодируется как двоичное 00001100 (при однобайтовом типе числа). Отрицательные целые числа часто кодируются в так называемом дополнительном коде, когда старший двоичный разряд используется как признак отрицательности числа, а остальные разряды должны быть такими, чтобы сумма отрицательного числа и его модуля равнялась нулю. Так, десятичное число –1 будет представлено как двоичное 1111111111111111 (при двухбайтовом типе числа). Минимально допустимое двухбайтовое число — 32768 кодируется как 1000000000000000, а максимальное 32767 — как 0111111111111111.
Для вещественных чисел система кодирования является более сложной. Обычно для каждого числа часть байтов отводится для хранения мантиссы числа, а часть — для порядка числа.
Изучение любого языка высокого уровня обычно начинается с освоения основных команд и написания первых простейших программ. Но с ассемблером так сразу не получится. Это объясняется тем, что программы на ассемблере напрямую манипулируют устройствами компьютера, в первую очередь процессором и памятью. Языки высокого уровня скрывают от программиста все манипуляции с компьютерным «железом». Таким образом, чтобы научиться программировать на ассемблере, необходимо знать архитектуру компьютера.
1.1. Архитектура компьютера.
Успешное применение языка ассемблера невозможно без знания и понимания архитектуры компьютера и знания архитектуры конкретного процессора, для которого будет создаваться программа.
Архитектура компьютера – это логическая организация, структура и ресурсы компьютера, которые может использовать программист.
Архитектура компьютера включает в себя архитектуры отдельных устройств, входящих в компьютер. Хотя компьютер состоит из многих внешних и внутренних устройств, но реально программисту на ассемблере приходится работать только с тремя устройствами компьютерной системы: процессором, памятью и портами ввода-вывода. В сущности, эти три устройства определяют работу всего компьютера и работу всех внешних устройств подключенных к нему. Все эти три устройства соединены между собой при помощи трех основных шин: шиной данных (ШД), шиной адреса (ША) и шиной управления (ШУ) (рис. 1).

Рис. 1. Архитектура ЭВМ.
Процессор — электронный блок либо интегральная схема (микропроцессор), исполняющая машинные инструкции (код программ), главная часть аппаратного обеспечения компьютера или программируемого логического контроллера.
Оперативная память предназначена для загрузки программ и для временного хранения различных данных, необходимых для работы программ.
Порты ввода-вывода предназначены для взаимодействия с пользователем и другими устройствами.
Шина (bus) – это группа параллельных проводников, с помощью которых данные передаются от одного устройства к другому:
- Шина данных (data bus) используется для обмена команд и данных между процессором и оперативной памятью, а также между устройствами ввода-вывода и ОЗУ.
- Шина управления (control bus) используется для передачи специальных сигналов, которые синхронизируют работу всех устройств, подключенных к системной шине. Например, процессор должен знать, когда можно читать информацию с шины данных. Для этого используется специальный сигнал готовности шины данных.
- Шина адреса (address bus) используется для указания адреса ячейки памяти в ОЗУ, к которой в текущий момент происходит обращение со стороны процессора или устройства ввода-вывода (чтение или запись).
Все три шины вместе образуют системную шину или ее еще называют магистраль.
1.2. Системы счисления.
Слово "компьютер" (computer) с английского языка переводится как "вычислитель", т. е. машина для проведения вычислений. И это полностью соответствует действительности, т. к. на уровне "железа" компьютер выполняет только простейшие арифметические операции с числами, такие как сложение и умножение.
Сердцем компьютера является процессор, называемый часто центральным процессором (ЦП) или микропроцессором. Именно центральный процессор выполняет все вычисления.
Так исторически сложилось, что практически все цифровые микросхемы, в том числе компьютерные процессоры, работают только с двумя разрешенными уровнями напряжения. Один из этих уровней называется уровнем логической единицы (или единичным уровнем), а другой — уровнем логического нуля (или нулевым уровнем). Чаще всего логическому нулю соответствует низкий уровень напряжения (от 0 до 0,4 В), а логической единице — высокий уровень (от 2,4 до 5 В). Два уровня напряжения было выбрано исключительно из-за простоты реализации.
Таким образом, можно образно представлять, что в электронной цепи компьютера "бегают" только цепочки ноликов и единичек. За этими цепочками нулей и единичек закрепилось название машинные коды. Точно также можно представлять, что в память компьютера, а также на магнитные, оптические и прочие носители записываются нолики и единички, которые в совокупности составляют хранимую информацию.
То есть компьютер способен воспринимать только нолики и единички, а для нас (людей) эти нолики и единички представляются через устройства вывода (дисплеи, принтеры, звуковые колонки и пр.) в виде текста, графических изображений и звуков.
Так как компьютер способен воспринимать только два управляющих сигнала: 0 и 1, то и любая программа должна быть ему представлена только в двоичных кодах, т. е. в машинных кодах. В старые добрые времена операторы первых ЭВМ программировали напрямую в машинных кодах, переключая специально предусмотренные для этого тумблеры, или пробивали двоичные коды на перфолентах и перфокартах, которые затем считывала ЭВМ и выполняла операции согласно этим кодам.
Однако записывать и запоминать огромные двоичные цепочки, первым программистам было неудобно, поэтому они стали вместо двоичной системы использовать другие системы счисления, например десятичную, восьмеричную или шестнадцатеричную. Для сравнения: двоичное число 11001000 будет представлено в десятичном виде как 200, а в восьмеричной и шестнадцатеричной соответственно как 310 и С8.
Стоит еще раз отметить, что недвоичные системы счисления первые программисты стали использовать исключительно для личного удобства. Компьютер не способен воспринимать десятичные, шестнадцатеричные или восьмеричные числа, а только и только двоичные коды!
Таким образом, операторы первых ЭВМ стали составлять свои программы в более удобной системе счисления (восьмеричной, шестнадцатеричной или другой), а потом переводить их в двоичный машинный код. Наибольшее распространение у первых программистов из всех систем счисления получила шестнадцатеричная система счисления, которая до сих пор является основной в компьютерном мире. И все из-за того, что в отличие от других систем счисления перевод из шестнадцатеричной системы счисления в двоичную систему и обратно осуществляется очень легко — вместо каждой шестнадцатеричной цифры, подставляется соответствующее четырехзначное двоичное число.
Хотя шестнадцатеричная система облегчила работу с машинными кодами, но создавать программу в шестнадцатеричном виде все равно очень не просто. В итоге родился язык ассемблера, который давал возможность писать программы на более понятном человеку языке и в то же время позволял легко переводить их в машинный код.
Язык ассемблера прозвали низкоуровневым языком, потому что он максимально приближен к машинному языку, а значит к "железу" компьютера. После языка ассемблера стали появляться высокоуровневые языки, такие как Бейсик, Паскаль, Фортран, Си, С++ и пр. Они еще более понятны человеку, но преобразование в машинный код высокоуровневых программ значительно сложнее, из-за чего размер кода, как правило, получается большим и менее быстрым по сравнению с ассемблерными программами.
Если операторы первых ЭВМ переводили свои программы в машинный код вручную, то сейчас эту работу выполняют специальные программы— трансляторы (англ, translator — переводчик). Для языков высокого уровня транслятор принято называть компилятором (англ, compiler — составитель, собиратель). Для языка ассемблера обычно тоже не используется слово транслятор, а говорят просто: "ассемблер". Таким образом, ассемблером называют, как язык программирования, так и транслятор этого языка.
Соответственно процесс работы ассемблера называют ассемблированием. Процесс работы компилятора называют компилированием. Процесс обратный ассемблированию, т. е. преобразование машинного кода в программу на языке ассемблера называют дизассемблированием.
1.3. Биты и байты.
Цифра в двоичной арифметике называется разрядом (или точнее "двоичным разрядом") и может принимать значение ноль или единица. В компьютерном мире вместо разряда часто употребляют название бит.
Таким образом, минимальной единицей информации в компьютерной системе является бит, который может принимать только значение 0 или 1. Однако минимальным объемом данных, которым позволено оперировать любой компьютерной программе является не бит, а байт. Байт состоит из восьми бит. Если программе нужно изменить значение только одного бита, то она все равно должна считать целый байт, содержащий этот бит. Биты в байте нумеруются справа налево от 0 до 7, при этом нулевой бит принято называть младшим, а седьмой — старшим (рис. 2).

Так как в байте всего восемь бит, а бит может принимать только два значения, то простой арифметический подсчет показывает, что байт может принимать до 2 8 =256 различных значений. Поэтому в байте могут быть представлены целые числа в диапазоне от 0 до 255, или числа со знаком от -128 до +127.
Однако не только байтами может оперировать компьютерная программа, но и более крупными единицами данных— словами, двойными словами и учетверенными словами. Слово состоит из двух байт, при этом биты с 0 по 7 составляют младший байт в слове, а биты с 8 по 15— старший (рис. 3). Понятно, что слово может принимать до 2 16 =65536 различных значений.

Двойное слово, как следует из самого названия, состоит из двух слов или четырех байт, а значит из 32-х бит, а два двойных слова составляют учетверенное слово (64 бита).
Существует еще более крупная единица, которая называется параграф и представляет собой 16 смежных байт.
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
- непозиционными (в этих системах значение цифры не зависит от ее позиции — положения в записи числа);
- позиционными (значение цифры зависит от позиции).
Непозиционные системы счисления
Примеры: унарная, римская, древнерусская и др.
Позиционные системы счисления
Основание системы счисления —
количество различных цифр, используемых в этой системе.
отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде
где i — номер разряда, а s — основание системы счисления.
Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:
По определению веса разряда
где i — номер разряда, а s — основание системы счисления.
Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
Например, для системы счисления с основанием 4:
1302.24 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 + 2⋅4 -1
Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:
1302.24 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 + 2⋅4 -1 =
= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =
= 64 + 48 + 2 + 0,5 = 114,5
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
- пронумеровать разряды исходного числа;
- записать сумму, слагаемые которой получаются как произведения очередной цифры на основание системы счисления, возведенное в степень, равную номеру разряда;
- выполнить вычисления и записать полученный результат (указав основание новой системы счисления — 10).
Вспомним пример перевода из системы счисления с основанием 4 в десятичную:
13024 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 = 114
Иначе это можно записать так:
114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 13024
Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно
Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры.
В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:

Меньше разрядов
(Написано разжевано, чтобы каждый смог понять суть этого пункта)
Возьмем число 10 в десятичной СС и переведем его в двоичную СС, получим 1010, переведем в троичную симметричную СС, получим +0+, ну а если в троичную несимметричную СС, то получим 101. Из этого мы видим, что в некоторых числах в троичной симметричной и несимметричной СС-ах меньше разрядов, чем в двоичной СС.
Возьмем число 5 в десятичной СС и переведем его в двоичную СС, получим 101, переведем в троичную симметричную СС, то получим +--, ну а если в троичную несимметричную СС, то получим 12. Из этого мы видим, что в некоторых числах в троичной несимметричной СС меньше разрядов, чем в двоичной и троичной симметричной СС-ах.
Емкость
Троичная СС вмещает больший диапазон чисел, т.к. 3^n>2^n (где n-натуральное число). Например, если n=9, то 3^9=19683>2^9=512.
3.
Читайте также:


